Eight theory modules in total. Five morning modules (3.5 hours each):
- M1: Classical 2D parallel and fan-beam FBP. (F. Noo)
- M3: Classical cone-beam theory. (R. Clackdoyle)
- M5: Helical cone-beam and advanced fan-beam theory. (F. Noo)
- M7: Modern reconstruction theory: DBP and Hilbert inversion. (L. Desbat)
- M9: Inverse problems perspective (interior/exterior/limited-angle problem, stability). (M. Defrise)
Three afternoon modules (3.5 hours each) partially overlapping with the computer "hands-on" sessions.
- M2: Discretization and sampling. (L. Desbat)
- M4: Introduction to Data Consistency Conditions. (M. Defrise)
- M8: DBP and Hilbert inversion for divergent geometries. (R. Clackdoyle)
Computer "hands-on" sessions (3 hours each).
- L1: 2D parallel FBP. (S. Rit)
- L2: 2D divergent FBP and 3D circular FBP. (S. Rit)
- L3: 2D parallel DBP. (S. Rit)
Participants will have the option to register either for all 8 theory modules, or for the 5 morning sessions and 3 "practical" computer sessions in the afternoons. The first hour of the afternoon sessions will be available for all participants.
Formal mathematical demonstrations will be given for all key theoretical results. Attendees intending to participate in the hands-on session will need to bring their own laptop computers. Jupyter notebooks will be used with the RTK software package. Windows, MacOS and Linux can be used. Installation instructions will be sent one month before the summer school.
The Friday afternoon sessions F1-F6 have not yet been finalized. They are likely to consist of short parallel sessions on specialized topics, and an optional course examination for participants requesting an "achievement certificate".
Program (subject to modification before or during the Summer School)
Sunday
– 16:00-19:00 : Check-in.
– 19:00 : Summer School opening (Chapelle lecture room).
– 19:30 : Dinner.
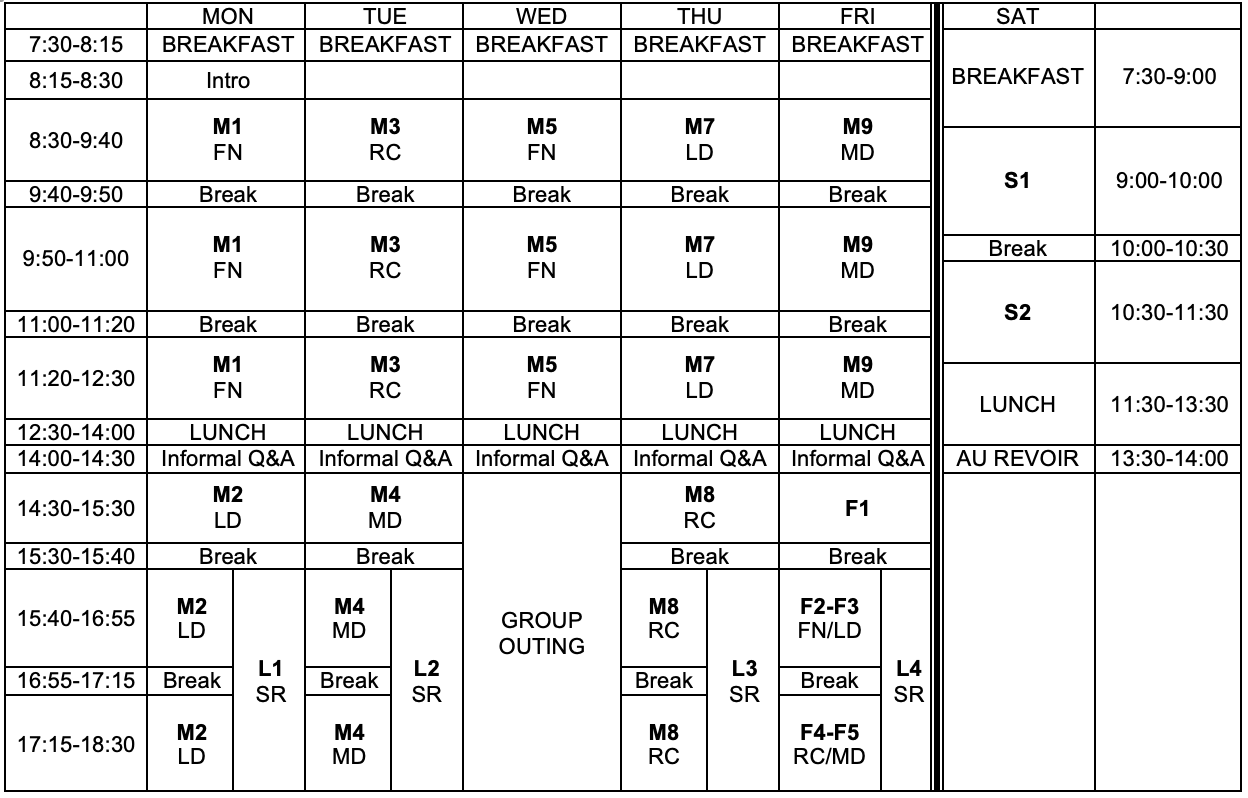
(FN: Frédéric Noo, LD: Laurent Desbat, SR: Simon Rit, RC: Rolf Clackdoyle, MD: Michel Defrise).
Outline of each module (provisional)
F1: Optional final examination. Others can form small informal groups for technical discussions with (or without) instructors.
F2 and F3: two lectures of 30 minutes each given by Frederic Noo and Laurent Desbat for “catchup” on course material or on selected supplementary topics.
F4 and F5: similarly to F2 and F3, two lectures of 30 minutes each given by Rolf Clackdoyle and Michel Defrise.
L4: optional computer lab time for completing your computer projects and/or informal "practical implementation" questions for Simon Rit.
S1, S2: small group technical workshops, possibly several in parallel, organized during the week with one or more of the instructors. Presentation of "Attendance Certificates" and "Achievement Certificates" to those requiring or requesting some official documentation.
M1. Classical 2D parallel and fan-beam FBP.
- Parallel projections and backprojection
- Fourier transforms and Fourier slice theorem
- Filtered backprojection (FBP)
- Fan-beam projections (circular trajectory)
- Fan-beam FBP
- Fan-beam short-scan
|
M2: Discretization and sampling.
- Fourier series, sampling, band-limit, Nyquist rate, Shannon sampling
- Exact sinc interpolation; over-sampled interpolation schemes
- "Essentially" band-limited functions
- 2D and 3D sampling; lattices, exact interpolation formulas
- Sampling the 2D Radon transform
|
L1: 2D parallel filtered backprojection.
- Simulate projections and reference data
- Visualize images (slices and profiles)
- Implementation of the backprojection
- Implementation of the ramp filter
- Implementation of 2D FBP
- Numerical validation of the Fourier slice theorem (if time permits)
|
M3. Classical cone-beam theory.
- 3D Radon transform and FBP inversion
- Cone-beam projections and "source" trajectories
- Tuy's condition
- Grangeat's result
- The shadow zone (circular trajectory)
- Cone-beam FBP (non-truncated projections)
- Feldkamp's algorithm
|
M4: Introduction to Data Consistency Conditions.
- Helgason-Ludwig (H-L) conditions (2D parallel case), polynomial form
- Consequence: Data Consistency Conditions (DCC)
- H-L conditions, inner-product formulation
- Other forms of DCC: frequency-distance relation
- Rebinning H-L conditions for circular fan-beam
- Pairwise DCC for fan-beam projections (arbitrary trajectory) using Hilbert projection equality
- H-L for 3D parallel projections (if time permits)
|
L2: 2D divergent FBP and 3D circular FBP.
- 2D fan-beam FBP
- Feldkamp's algorithm (circular cone-beam FBP)
- Validation of the properties of Feldkamp's algorithm
- Short scan (if time permits)
- Offset detector (if time permits)
|
M5: Helical cone-beam and advanced fan-beam theory.
- Helical trajectory; short object problem; long object problem
- Pi-lines; Tam-Danielsson detector window; helical pitch
- Katsevich FBP algorithm
- Conventional fan-beam shortscan (Parker weights)
- Fan-beam 'super-shortscan' and the Hilbert projection equality
- Virtual fan-beam trajectories and truncated projections (if time permits)
M7: Modern reconstruction theory: DBP and Hilbert inversion.
- Hilbert transform and inverse, and 2D Hilbert transform
- Inversion of the 2-sided truncated Hilbert transform; assumptions on function support
- 2D differentiated backprojection (DBP), definition and Hilbert image equality
- Field-of-view (FOV) defined by finite detector extent; object support
- DBP reconstruction algorithm, paying attention to object support conditions
- DBP at arbitrary starting angle
- 3D parallel projections and 3D parallel DBP (if time permits)
|
M8: DBP and Hilbert inversion for divergent geometries.
- Fan-beam DBP, and the sum of two Hilbert transforms
- Reconstruction from fan-beam DBP
- DBP for cone-beam
- Chords / pi-lines; the challenge of cone-beam DBP
- Helix; long-object problem; existence of pi-lines (review)
- Long-object problem via DBP and 2-sided Hilbert transform
- DBP with M-lines
|
L3: 2D parallel DBP.
- Differentiated backprojection
- Finite Hilbert inverse
- Half-pixel shift
- Region-of-interest simulation and reconstruction
|
M9: Inverse problems perspective.
- Continuous linear operators (in general); stability
- Example of invertible matrix (uniqueness ok) but unstable
- Limited-angle data (classical 2D projections)
- Interior problem (classical 2D projections)
- Exterior problem (classical 2D projections)
- Relevance and stability of 1-sided truncated Hilbert transform
- Interior problem in 3D; other news for the interior problem (if time permits)



